Interpret the Direction of the Gradient Vector at a Point.
Conversely a negative gradient vector points in the direction of greatest decrease. Mar 26 2014 at 800.

Partial Derivatives And The Gradient Of A Function Youtube
Interpret the direction of the gradient vector at a point.
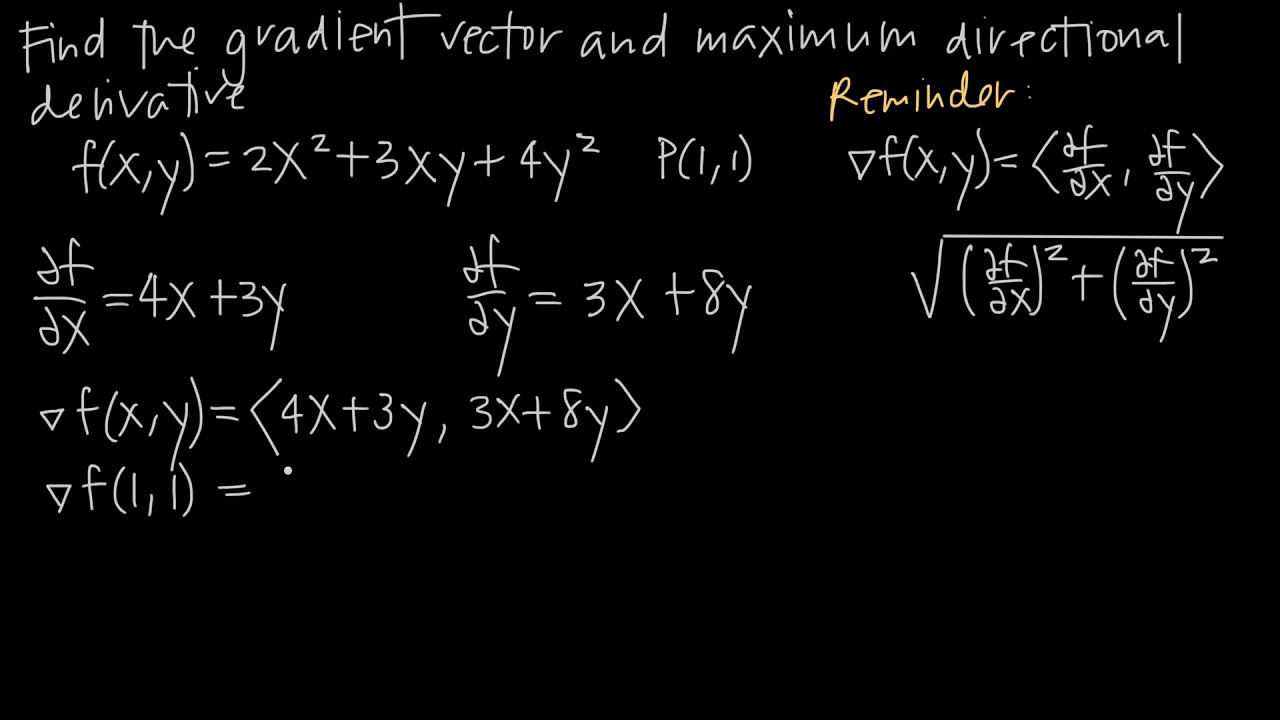
. Choose the correct answer below. Gradient is slope along purely x slope along purely y when we represent it in graph we can see that vector moves toward x axis as slope along purely x increases ie vector will point in resultant of balanced slopes along x y which will be steepest Am I correct 3 votes ciramos602 4 years ago at 650. Interpret the direction of the gradient vector at a point.
Slope of tangent line O D. In the second case the value of is minimized. What is this going going to represent with ingredient of a function at a given point is going to be a vector in pointing in the direction of the fastest increase and whose magnitude represents this rate of increase.
The gradient of the scalar function evaluated at a point gives the maximum rate of change of the function at that point. And when you want to interpret the gradient vector. Steepness of the slope at that point O C.
Think of the equal height contours on a topographical map. Therefore the directional derivative is equal to the magnitude of the gradient evaluated at multiplied by Recall that ranges from to If then and and both point in the same direction. The gradient is therefore called a direction of steepest ascent for the function f x and the negative of the gradient is called the direction of steepest descent.
The main purpose of gradient descent is to minimize an error or cost most notably prevalent in machine learning. The gradient of H at a point is a plane vector pointing in the direction of the steepest slope or grade at that point. Direction of unit vector B.
Slope of tangent line D. Direction of steepest ascent. In the first case the value of is maximized.
Interpret the direction of the gradient vector at a point. Now if you consult your third example image the angles reported by imgradient are indeed correct. Uh and so the direction um represents the of the greedy and represents the direction of steepest ascent from that point.
Direction of unit vector O B. Interpreting the gradient After completing this section students should be able to do the following. F x 4 x 3.
Direction of unit vector OB. We know that the gradient vector points in the direction of greatest increase. The gradient vector at a particular point in the domain is a vector whose direction captures the direction in the domain along which changes to are concentrated and whose magnitude is the directional derivative in that direction.
Um so we know therefore that the magnitude of the Grady int which is the partial derivative in. Recognize that the gradient points in the initial direction of greatest increase of the functions value. The magnitude of the gradient will determine how fast the temperature rises in that direction.
F x 2 y 2 z 2. Fxx ydx x2y2 x x2y2 x2x x2y22 y2x2 x2y22 fyx ydy x2y2 x 2xyx2y22 The gradient is then rf12 4 124 12 4 1 43 42525 We now find the magnitude ofvWeget p925p v 34 The directional derivative is then 25h3 4i. Concepts Through Functions A Unit Circle Approach to Trigonometry 4th Edition In Problems 37-48 determine algebraically whether each function is even odd or neither.
Which of course is a vector that points away from the center. If you remember in the video about how to interpret the gradient in the context of a graph I said it points in the direction of steepest descent. Slope of tangent line C.
This is obviously increasing in the direction away from the center. Imagine you have a function modeling costs for your company. This makes sense because the gradient direction corresponds to the direction towards the greatest rate of change.
Choose the correct answer below. Choose the correct answer below. Consider a surface whose height above sea level at point x y is Hx y.
Well when we take the Grady int gonna get the radiant of tea is equal to lets say f one of x comma y f two of x comma y. Interpret the magnitude of the gradient vector at a point Choose the correct answer below. If the gradient vector of exists at a point then we say that is differentiable at that point.
The disappears because is a unit vector. Reconize that the gradient is normal to level sets. First we find the gradient.
The equation of line with slope m3 and passing through the point 52. I used the directional derivative to demonstrate because once you pick a direction the derivative always just tells you the rate of change. -135 degrees means that were pointing to the south west which does make sense as we are progressing from dark pixels to light pixels.
A particularly important application of the gradient is that it relates the electric field intensity to the electric potential field. Add a particular point. The rate of increase of the function in the direction of steepest ascent at the point OB.
Steepness of the slope at that point. And you know it might not be a perfect straight line. Compute the gradient vector of a function of several variables.
Direction of steepest ascent C. Direction of steepest ascent OD. The rate of increase of the function along the level curve at the.
The direction of steepest ascent at the point O C. So we know that the ingredient vector represents theme ingredient represented vector of all the personal derivatives of the function. F 2 x 2 y 2 z.
Steepness of the slope at that point. This is a vector function that involves both magnitude and direction. The direction along the level curve at the point OD.
If then and and point in opposite directions. But the more you zoom in the more it looks like a straight line. In the direction of vh35iat the point12.
The gradient of a scalar field is a vector that points in the direction in which the field is most rapidly increasing with the scalar part equal to the rate of change. These properties show that the gradient vector at any point x represents a direction of maximum increase in the function f x and the rate of increase is the magnitude of the vector.

Tj Limits And Continuity A Study Of Limits And Continuity In Multivariable Calculus Yields Many Counter Calculus Partial Differential Equation Calculate Area

Directional Derivatives And The Gradient

Flying Dragon Vinyl Decal Sticker V1 Wyvern Medieval Fantasy Etsy In 2022 Dragon Silhouette Black Dragon Tattoo Dragon Tattoo Art

Gradient And Contour Maps Youtube

The Gradient Vector Multivariable Calculus Article Khan Academy

How To Find The Directional Derivative And The Gradient Vector Youtube

Show The Gradient To A Surface Using 3d Calc Plotter Youtube

Vector Calculus Understanding The Gradient Betterexplained

Gradient Definition Explanation And Examples Cuemath

Pin On Save The Date Enclosure Card

Across The Pond Shawl Pattern By Knitting Expat Designs Pattern Knitting Shawl Pattern

Effortless Optimization Through Gradient Flows Machine Learning Research Blog

Calculus What S The Geometrical Interpretation Of The Magnitude Of Gradient Generally Mathematics Stack Exchange

Gradient Of A Line Gcse Maths Steps Examples Worksheet
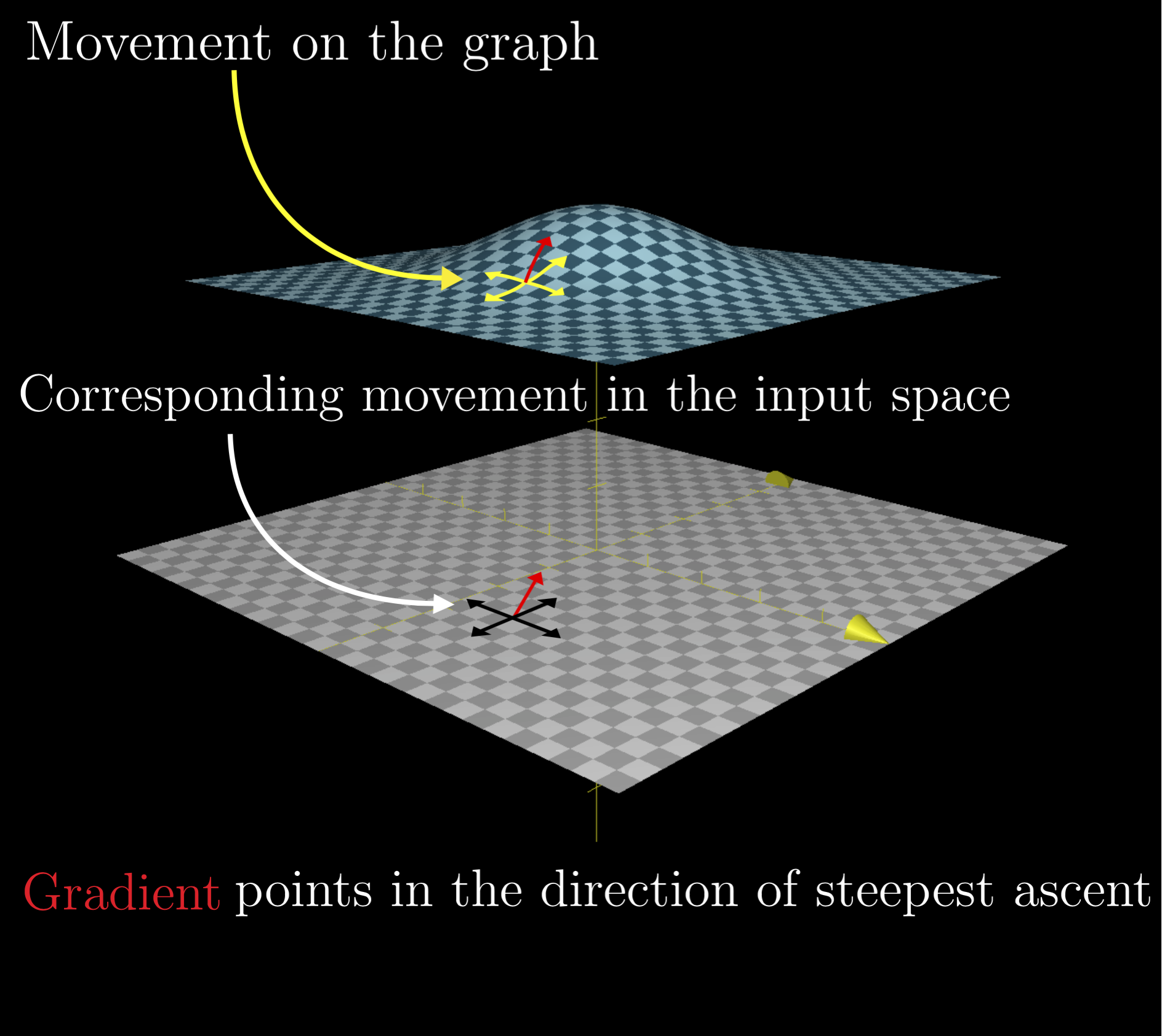
The Gradient Vector Multivariable Calculus Article Khan Academy

Directional Derivatives And The Gradient Calculus Volume 3
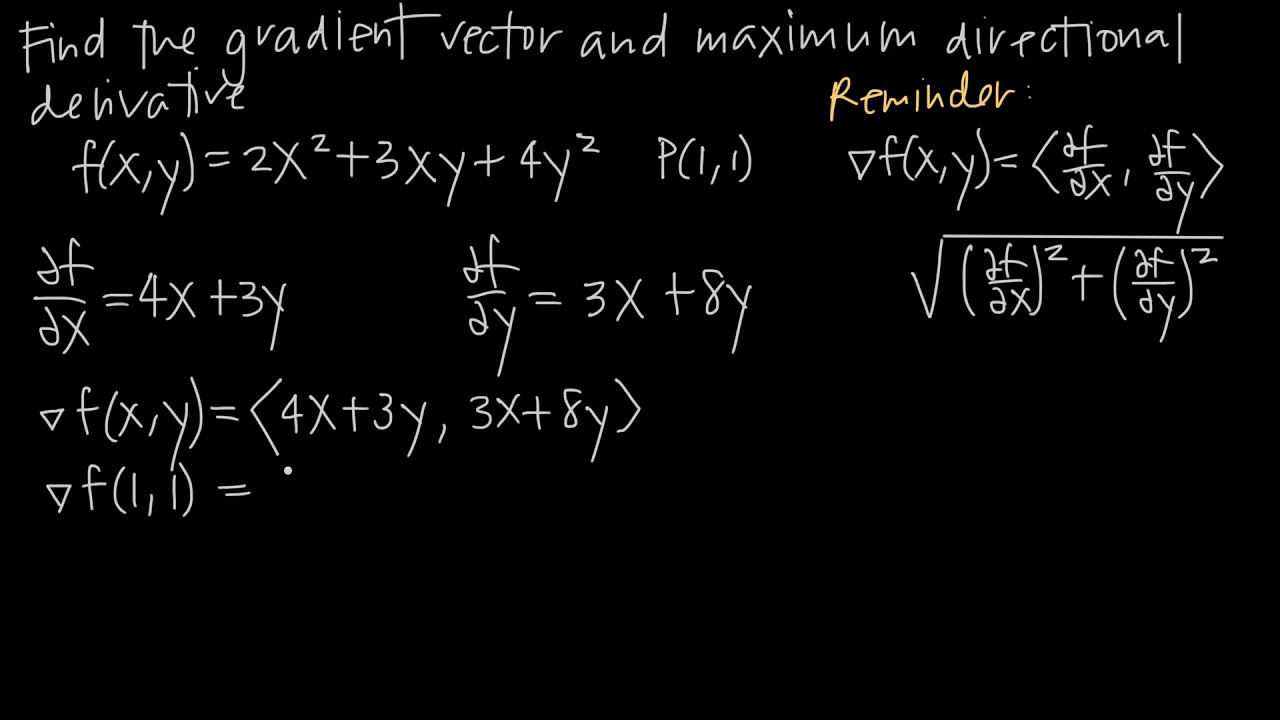
Finding Gradient Vectors For Multivariable Functions Krista King Math Online Math Help
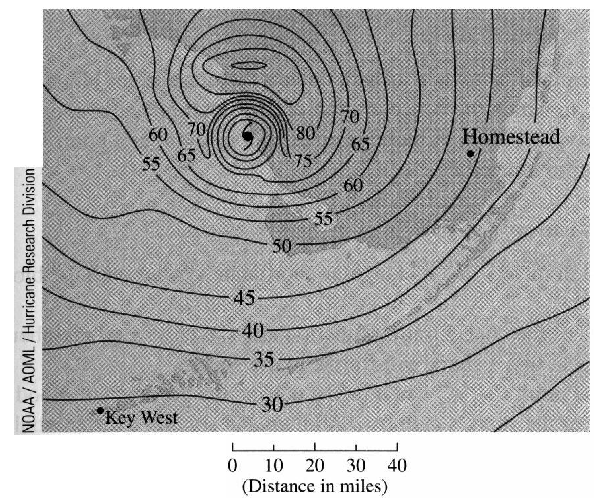
Comments
Post a Comment